Perbandingan Segmen Garis

PERBANDINGAN SEGMEN GARIS

Apakah kau punya penggaris panjang? Penggaris mana yang kau miliki? Penggaris berskala 20 cm atau 30 cm? Jika belum punya, silahkan pinjam ke kawan sebangku dan kumpulkan kedua penggaris itu. Jika kedua penggaris itu mempunyai ukuran panjang yang berbeda, bisakah kau menyebutkan berapa perbandingannya? Agar kau sanggup menjawabnya, yuk simak topik ini dengan saksama.

Sebelum kau menuntut ilmu wacana perbandingan segmen garis, mari kita ingat kembali definisi garis.

Garis

Suatu garis terbentuk dari relasi antara dua titik yang tidak berhimpit dan membentuk garis lurus. Suatu garis tak mempunyai ujung atau pangkal. Jika sebuah garis mempunyai pangkal namun tidak berujung, dinamakan sinar garis, sedangkan jikalau sebuah garis mempunyai pangkal dan ujung, dinamakan ruas garis. Penamaan sebuah garis sanggup dituliskan menggunakan karakter kecil seperti g, h, k, l dan sebagainya, sedangkan penamaan untuk ruas garis sanggup dituliskan nama titik penyusunya.

Nah, kini kau niscaya sudah ingat kembali definisi garis. Selanjutnya, mari kita menuntut ilmu wacana perbandingan segmen garis.

Perbandingan Segmen Garis

Suatu garis sanggup dibagi menjadi n bagian sama panjang atau dengan perbandingan tertentu. Agar lebih jelas, amati gambar berikut ini.

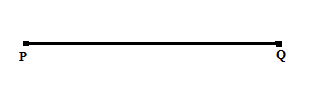
          Ruas garis PQ dan ruas garis QP yakni ruas garis yang serupa alasannya yakni keduanya ialah himpunan titik-titik yang sama, sehingga sanggup ditulis PQ = QP. Jika pada ruas garis PQ kita sisipkan titik O, maka terdapat 2 segmen garis yakni PO dan OQ.

          Jika berlaku PO = OQ, maka O ialah titik tengah ruas garis PQ dengan perbandingan PO : OQ = 1 : 1. Dengan demikian, kita sudah membagi ruas garis PQ menjadi nbagian sama panjang, dengan n = 2. Kita juga sanggup membagi ruas garis PQ dengan perbandingan tertentu, yakni dengan menyisipkan titik O di antara ruas garis PQ dengan perbandingan PO : OQ sesuai dengan yang kita kehendaki atau membaginya menjadi beberapa segmen garis.

Selanjutnya, amati beberapa segmen garis berikut.

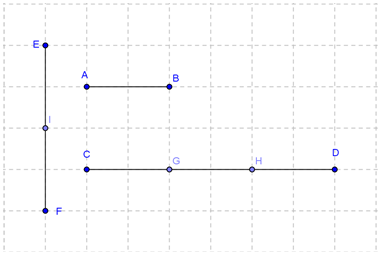
          Panjang AB = 2 satuan panjang, panjang CD = 6 satuan panjang dan panjang EF = 4 satuan panjang. Perbandingan segmen garis AB dan segmen garis CD sama dengan satu banding tiga, ditulis AB : CD = 1 : 3. Dapat juga dinyatakan dengan 3AB = CD. Perbandingan segmen garis AB dan segmen garis EF sama dengan satu banding dua, ditulis AB : EF = 1 : 2. Dapat juga dinyatakan dengan 2AB = EF. Selanjutnya, perbandingan segmen garis CG dan segmen garis CD sama dengan satu banding tiga, ditulis CG : CD = 1 : 3. Dapat juga dinyatakan dengan 3CG = CD.

Mudah sekali, kan? Agar kalian lebih paham, amati teladan di bawah ini.

Contoh

Contoh 1:

Perbandingan ruas garis AB : AC = 2 : 3. Jika panjang AB = 4 cm, maka panjang AC yakni ....

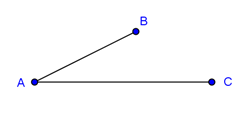
Penyelesaian:

Perhatikan bahwa AB : AC = 2 : 3 atau sanggup dinyatakan sebagai ABAC=23$\frac{AB}{AC}=\frac{2}{3}$. Dengan demikian, diperoleh:

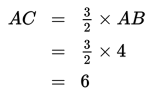
Jadi, panjang AC yakni 6 cm.

Contoh 2:

Pada ruas garis AB, terletak titik P di antara A dan B, sehingga AP : PB = 1 : 5. Jika panjang AB = 12 cm, maka panjang AP adalah...

Penyelesaian:

Diketahui titik P berada di antara A dan B, sehingga AB = AP + PB. Oleh alasannya yakni AP : PB = 1 : 5, maka AB = AP + PB = 6 . Dengan demikian, AP : AB = 1 : 6 atau sanggup dinyatakan sebagai APAB=16$\frac{AP}{AB}=\frac{1}{6}$. Dengan demikian, diperoleh:

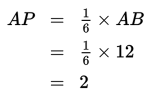
Jadi, panjang AP yakni 2 cm.

Contoh 3:

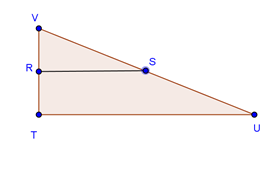
Pada gambar di atas, diketahui RS // TU. Jika UV = 9 cm, VT = 6 cm, VS = 3 cm dan UV : VS = VT : VR. Tentukan panjang VR.

Penyelesaian:

Berdasarkan gunjingan dari soal, diperoleh:

UV : VS = VT : VR

Dengan demikian, sanggup ditulis menjadi UVVS=VTVR$\frac{UV}{VS}=\frac{VT}{VR}$. Dengan demikian, diperoleh:

Jadi, panjang VR yakni 2 cm.