Kedudukan Dua Garis

Pernahkah kalian mengikuti kontes baris-berbaris untuk kegiatan 17 Agustus? Atau cuma sekadar menonton pasukan baris-berbaris? Jika diperhatikan, kegiatan baris-berbaris terdiri atas 3 atau 4 banjar ke belakang. Salah satu penilaiannya yakni kerapian dalam menyusun barisan. Tiap banjar mesti menjaga banjarnya mudah-mudahan senantiasa membentuk garis lurus dan jaraknya senantiasa konstan antar banjar. Pada kendala ini, kalian sanggup mengamati bahwa kedua banjar barisan tersebut tidak pernah berpotongan, senantiasa sejajar dengan jarak yang sama. Kedua banjar barisan tersebut sanggup kita misalkan dua buah garis lurus, sehingga keduanya tidak saling berpotongan dan disebut garis sejajar.

        Permasalahan tersebut ialah salah satu referensi dari kedudukan dua garis. Apakah kedudukan garis cuma sejajar? Untuk tahu jawabannya, yuk simak topik ini dengan seksama.

        Sebelum kalian belajar mengenai kedudukan dua garis, kalian perlu mengerti apalagi dulu pengertian suatu garis. Untuk itu, mari kita simak klarifikasi berikut ini.

Garis

Suatu garis terbentuk dari kekerabatan antara dua titik yang tidak berhimpit dan membentuk garis lurus. Suatu garis tidak punya ujung atau pangkal. Jika suatu garis memiliki pangkal namun tidak berujung, dinamakan sinar garis, sedangkan jikalau suatu garis memiliki pangkal dan ujung, dinamakan ruas garis. Penamaan suatu garis sanggup dituliskan menggunakan abjad kecil seperti g, h, k, l dan sebagainya, sedangkan penamaan untuk ruas garis sanggup dituliskan nama titik penyusunya.

Perhatikan gambar berikut ini.

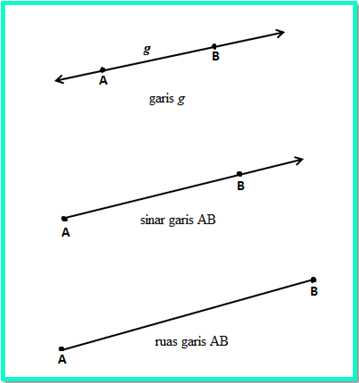
Kalian pasti sudah paham mengenai pengertian garis. Sekarang, mari kita belajar mengenai kedudukan dua garis.

Misalkan diberikan dua buah garis yaitu m dan n. Sifat-sifat kedudukan dua garis tersebut yakni selaku berikut. 

Dua Garis Sejajar

Garis m dan n dikatakan sejajar jikalau kedua garis itu tidak pernah berpotongan di titik manapun walaupun diperpanjang hingga tak berhingga. Dua garis yang sejajar dinotasikan dengan ” // ” dan senantiasa sanggup diposisikan pada bidang yang sama.

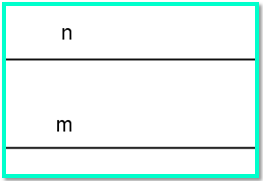
Dua Garis Berpotongan

Garis m dan n dikatakan saling berpotongan apabila garis tersebut terletak pada satu bidang datar dan memiliki satu titik potong atau titik persekutuan.

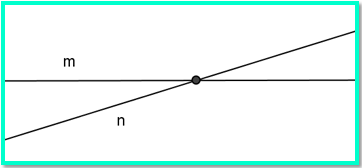
Dua Garis Berimpit

Garis m dan n dikatakan saling berimpit apabila garis tersebut terletak pada satu garis lurus pada suatu bidang. Syarat minimal dua garis berimpit yakni dua titik pada masing-masing garis saling berimpit.

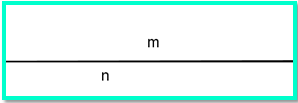
Dua Garis Bersilangan

Garis m dan n dikatakan bersilangan apabila garis-garis tersebut tidak terletak pada satu bidang datar dan tidak akan berpotongan apabila diperpanjang.

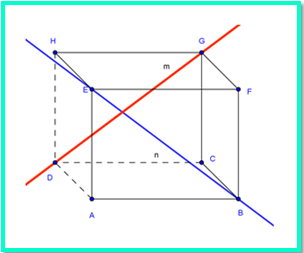
Garis m terletak pada bidang DCGH dan garis n terletak pada bidang ABFE. Garis m dan garisn saling bersilangan.

Materi tersebut cukup menghasilkan kalian paham bukan? Untuk memperbesar pengertian kalian, amati referensi berikut ini.

Contoh

Contoh 1:

Diketahui kubus ABCD.EFGH. Kemungkinan kedudukan garis-garis diagonal bidang pada masing masing segi kubus yakni ....

Penyelesaian:

Perhatikan gambar kubus ABCD.EFGH berikut ini.

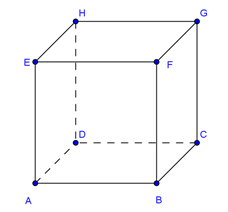
Misalkan diambil salah satu diagonal bidang yaitu AC.

Diagonal bidang AC akan berpotongan dengan diagonal bidang BD pada bidang ABCD.

Diagonal bidang AC akan sejajar dengan diagonal bidang EG pada bidang ACGE.

Diagonal bidang AC akan bersilangan dengan diagonal bidang FH pada bidang EFGH.

Dengan demikian, untuk setiap diagonal bidang pada kubus senantiasa sanggup didapatkan garis lain yang sejajar, berpotongan dan bersilangan.

Contoh 2:

Diberikan garis k, l, m. Jika garis k sejajar dengan garis m dan garis m sejajar dengan garis l, maka kemungkinan kedudukan garis k dan l adalah ....

Penyelesaian:

Ada 2 kemungkinan, yaitu:

Pada kendala 1, garis k akan sejajar dengan garis l.
Pada kendala 2, garis k akan berimpit dengan garis l.
Garis k dan l tidak akan berpotongan dan bersilangan.

Contoh 3:

Perhatikan berdiri layang-layang berikut ini.

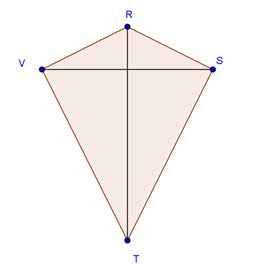
Jika ruas garis TV dan RS diperpanjang, maka kedudukan kedua garis yakni ....

Penyelesaian:

Perhatikan bahwa RSTV merupakan berdiri layang-layang sehingga ruas garis TV dan RStidak sejajar.

Dengan demikian, jikalau ruas garis TV dan RS diperpanjang maka kedua garis akan berpotongan di suatu titik.