Komplemen Sebuah Himpunan

Komplemen Suatu Himpunan

        Agar kalian sanggup mengerti dengan baik perihal operasi perhiasan pada sebuah himpunan, coba kalian ingat kembali pengertian himpunan semesta. Apakah kalian telah mengingatnya? Kalau sudah, mari amati klarifikasi berikut ini.

        Komplemen dari sebuah himpunan A adalah himpunan yang anggota-anggotanya di dalam himpunan semesta S dan bukan anggota dari himpunan A.

        Komplemen dari sebuah himpunan A dinotasikan dengan A' atau Ac (dibaca: komplemen A) dan didefinisikan selaku berikut.

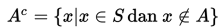
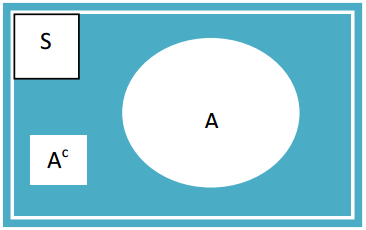
        Bila dinyatakan dalam diagram Venn, himpunan A dan himpunan Ac dapat digambarkan seumpama berikut.

◈ Contoh Komplemen Suatu Himpunan ◈

Contoh 1:

Diketahui himpunan semesta S = {1, 2, 3, 4, ..., 10} dan himpunan E = {2, 4, 6, 8, 10}. Tentukan himpunan dari Ec.

Penyelesaian:

Perhatikan dua himpunan tersebut. Untuk membuat lebih mudah dalam menentukan Ec, kalian sanggup menuliskan kembali secara lengkap himpunan S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, lalu kalian hilangkan anggota yang serupa dengan himpunan E yaitu 2, 4, 6, 8, 10. Sekarang, anggota Stinggal 1, 3, 5, 7, 9. Anggota S yang tersisa inilah yang merupakan Ec.

Jadi, Ec = {1, 3, 5, 7, 9}.

Contoh 1:

Diketahui:

S = himpunan huruf-huruf vokal

F = himpunan huruf-huruf konsonan

tentukan solusi dari Fc.

Penyelesaian:

Fc adalah himpunan huruf-huruf huruf selain huruf konsonan, maka anggota dari Fc adalah huruf-huruf vokal yaitu a, i, u, e, o. Jadi, Fc = himpunan huruf-huruf vokal.

Contoh 1:

Diketahui:

S = himpunan bilangan cacah

G = himpunan bilangan asli

tentukan anggota dari Gc.

Penyelesaian:

S = himpunan bilangan cacah maka S = {0, 1, 2, 3, ...}

G = himpunan bilangan asli maka S = {1, 2, 3, 4, ...}

Gc adalah himpunan anggota di S yang bukan anggota di G, yaitu 0.

Jadi, anggota himpunan Gc adalah 0.