Contoh Soal Sifat-Sifat Segiempat

Contoh 1.

Mari amati jajargenjang EFGH berikut.

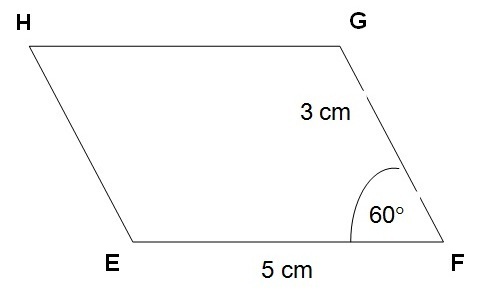
Coba tentukan:

a. Panjang segi HG dan EH; serta

b. Besar ∠HEF, ∠EHG, dan ∠HGF.

Penyelesaian:

a. Pada jajargenjang EFGH tersebut, terlihat bahwa:

• HG berhadapan dengan EF sehingga panjang HG = panjang EF = 5 cm; dan
• EH berhadapan dengan FG sehingga panjang EH = panjang FG = 3 cm.

Jadi, panjang segi HG merupakan 5 cm dan panjang segi EH merupakan 3 cm.

b. Pada jajargenjang EFGH tersebut, ∠HEF berdekatan dengan ∠EFG sehingga:

∠HEF + ∠EFG = 180°

∠HEF + 60° = 180°           Dari gambar dikenali ∠EFG = 60°

∠HEF = 180° - 60° = 120°

Coba amati kembali jajargenjang EFGH tersebut.

Pada jajargenjang EFGH tersebut, terlihat bahwa:

• ∠EHG berhadapan dengan ∠EFG sehingga ∠EHG = ∠EFG = 60°; dan
• ∠HGF berhadapan dengan ∠HEF sehingga ∠HGF = ∠HEF = 120°.

Jadi, ∠HEF =120°, ∠EHG = 60°, dan ∠HGF = 120°.

Contoh 2.

Coba lengkapi sudut-sudut pada trapesium berikut.

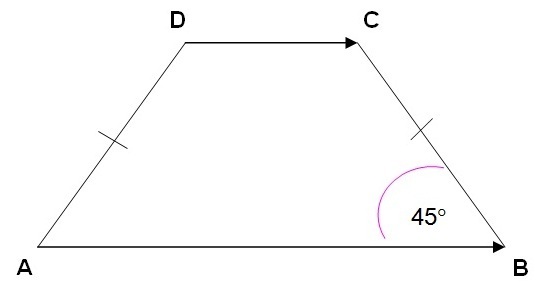
Penyelesaian:

Pada trapesium ABCD, AB sejajar dengan DC.

Sudut-sudut yang berdekatan di antara dua segi sejajar itu merupakan ∠ABC dengan ∠BCD dan ∠BAD dengan ∠ADC.

Dari uraian ini, kau mendapat ∠ABC + ∠BCD = 180° dan ∠BAD + ∠ADC = 180°.

∠ABC + ∠BCD = 180°

45° + ∠BCD = 180°
∠BCD = 180° - 45° = 135°                 Dari gambar dikenali ∠ABC = 45°

Sekarang, coba amati kembali trapesium ABCD.

Trapesium ABCD merupakan trapesium samakaki dengan segi ganjal AB dan segi atas DC.

Sudut-sudut pada segi ganjal merupakan ∠ABC dan ∠BAD. Berdasarkan sifat trapesium haruslah ∠BAD = ∠ABC sehingga ∠BAD = 45°.

Sementara itu, sudut-sudut pada segi atasnya merupakan ∠ADC dan ∠BCD. Berdasarkan sifat trapesium haruslah ∠ADC = ∠BCD sehingga ∠ADC = 135°.